佩亚诺型的泰勒公式 - 万物之理：从计数到宇宙的数学地图

根据您提供的图片内容，我将为您整理关于“佩亚诺（Peano）型余项的泰勒公式”的相关知识、推导、图例解析以及一个额外生成的实例。

一、知识背景与前因后果 (为什么需要泰勒公式？)

在数学分析中，我们经常遇到复杂的函数。为了简化计算和理论分析，一个核心思想是用简单的函数去逼近复杂的函数。

最简单的逼近： 多项式函数（ $p (x) = a_{0} + a_{1} x + \dots + a_{n} x^{n}$ ）是各种函数中最简单的一种，它们的计算（加减乘）和分析（求导、积分）都非常容易。
逼近的起点 (一阶逼近)： 正如图片 image_8b4efc.png 中提到的，如果函数 $f (x)$ 在 $x_{0}$ 点可导，我们就可以用它在该点的切线（一个一次多项式）来近似 $f (x)$ ： $f (x) = f (x_{0}) + f^{'} (x_{0}) (x - x_{0}) + o (x - x_{0})$ 这里的 $o (x - x_{0})$ (读作“ $(x - x_{0})$ 的高阶无穷小”) 表示一个当 $x \to x_{0}$ 时，比 $(x - x_{0})$ 更快地趋向于 0 的误差项。
追求更高精度 (n 阶逼近)： 一次逼近（切线）通常不够精确。我们希望用一个 $n$ 次多项式 $T_{n} (x)$ 来逼近 $f (x)$ ，并要求这个多项式在 $x_{0}$ 点的函数值及其前 $n$ 阶导数值，都与 $f (x)$ 完全相同。 $T_{n}^{(k)} (x_{0}) = f^{(k)} (x_{0}), for k = 0, 1, \dots, n$
泰勒多项式诞生： 正如图片 image_8b4efc.png 所推导的，为了满足上述条件，这个 $n$ 次多项式 $T_{n} (x)$ 必须具有唯一的形式，即泰勒多项式： $T_{n} (x) = f (x_{0}) + f^{'} (x_{0}) (x - x_{0}) + \frac{f ^{''} ( x _{0} )}{2 !} (x - x_{0})^{2} + \dots + \frac{f ^{(n)} ( x _{0} )}{n !} (x - x_{0})^{n}$ $T_{n} (x) = k = 0 \sum n \frac{f ^{(k)} ( x _{0} )}{k !} (x - x_{0})^{k}$

这是一个非常棒的问题！泰勒公式的推导过程是微积分中最巧妙、最重要的思想之一。

它不是一个灵光一闪的“猜想”，而是基于一个非常直观和合理的目标推导出来的。

核心思想：用简单的多项式“冒充”复杂的函数

我们的目标是：能否找到一个 $n$ 阶多项式 $P_{n} (x)$ ，让它在某一点 $x_{0}$ 附近，尽可能地“像”一个复杂的函数 $f (x)$ ？

“像”是一个很模糊的词。在数学中，我们可以把它定义为：

第0步“像”： 在 $x_{0}$ 点，函数值相等。 $P_{n} (x_{0}) = f (x_{0})$ 。
第1步“像”： 在 $x_{0}$ 点，斜率（一阶导数）相等。 $P_{n}^{'} (x_{0}) = f^{'} (x_{0})$ 。
第2步“像”： 在 $x_{0}$ 点，凹凸性（二阶导数）相等。 $P_{n}^{''} (x_{0}) = f^{''} (x_{0})$ 。
...
第n步“像”： 在 $x_{0}$ 点，直到 $n$ 阶导数都相等。 $P_{n}^{(n)} (x_{0}) = f^{(n)} (x_{0})$ 。

如果我们能造出这样一个 $P_{n} (x)$ ，它在 $x_{0}$ 点的函数值、斜率、凹凸性……等等所有局部特性都和 $f (x)$ 完全一样，那么我们就可以理直气壮地说： $P_{n} (x)$ 是 $f (x)$ 在 $x_{0}$ 附近的“最佳 $n$ 阶替身”。

我们把这个待求的 $n$ 阶多项式写成最适合在 $x_{0}$ 点展开的形式： $P_{n} (x) = a_{0} + a_{1} (x - x_{0}) + a_{2} (x - x_{0})^{2} + a_{3} (x - x_{0})^{3} + \dots + a_{n} (x - x_{0})^{n}$ 我们的目标就是利用上面提出的 $n + 1$ 个“相等”条件，来求出 $a_{0}, a_{1}, a_{2}, \dots, a_{n}$ 这 $n + 1$ 个未知系数。

我们开始求解：

1. 求 $a_{0}$ (使用第0步条件： $P_{n} (x_{0}) = f (x_{0})$ )

将 $x = x_{0}$ 代入 $P_{n} (x)$ ： $P_{n} (x_{0}) = a_{0} + a_{1} (x_{0} - x_{0}) + a_{2} (x_{0} - x_{0})^{2} + \dots$ $P_{n} (x_{0}) = a_{0} + 0 + 0 + \dots$ 所以 $P_{n} (x_{0}) = a_{0}$ 。根据条件 $P_{n} (x_{0}) = f (x_{0})$ ，我们得到： $a_{0} = f (x_{0})$

2. 求 $a_{1}$ (使用第1步条件： $P_{n}^{'} (x_{0}) = f^{'} (x_{0})$ )

首先，对 $P_{n} (x)$ 求一阶导数： $P_{n}^{'} (x) = 0 + a_{1} + 2 a_{2} (x - x_{0}) + 3 a_{3} (x - x_{0})^{2} + \dots + n a_{n} (x - x_{0})^{n - 1}$ 将 $x = x_{0}$ 代入 $P_{n}^{'} (x)$ ： $P_{n}^{'} (x_{0}) = a_{1} + 2 a_{2} (0) + 3 a_{3} (0) + \dots$ $P_{n}^{'} (x_{0}) = a_{1}$ 根据条件 $P_{n}^{'} (x_{0}) = f^{'} (x_{0})$ ，我们得到： $a_{1} = f^{'} (x_{0})$

3. 求 $a_{2}$ (使用第2步条件： $P_{n}^{''} (x_{0}) = f^{''} (x_{0})$ )

对 $P_{n}^{'} (x)$ 再求导，得到二阶导数： $P_{n}^{''} (x) = 0 + 2 a_{2} + 3 \cdot 2 a_{3} (x - x_{0}) + \dots + n (n - 1) a_{n} (x - x_{0})^{n - 2}$ 将 $x = x_{0}$ 代入 $P_{n}^{''} (x)$ ： $P_{n}^{''} (x_{0}) = 2 a_{2} + 0 + 0 + \dots$ $P_{n}^{''} (x_{0}) = 2 a_{2}$ 根据条件 $P_{n}^{''} (x_{0}) = f^{''} (x_{0})$ ，我们得到 $2 a_{2} = f^{''} (x_{0})$ ，即： $a_{2} = \frac{f ^{''} ( x _{0} )}{2} = \frac{f ^{''} ( x _{0} )}{2 !}$

4. 求 $a_{3}$ (使用第3步条件： $P_{n}^{'''} (x_{0}) = f^{'''} (x_{0})$ )

对 $P_{n}^{''} (x)$ 再求导： $P_{n}^{'''} (x) = 3 \cdot 2 \cdot 1 a_{3} + \dots + n (n - 1) (n - 2) a_{n} (x - x_{0})^{n - 3}$ 将 $x = x_{0}$ 代入 $P_{n}^{'''} (x)$ ： $P_{n}^{'''} (x_{0}) = 3 \cdot 2 \cdot 1 a_{3} + 0 + \dots$ $P_{n}^{'''} (x_{0}) = 6 a_{3} = 3! a_{3}$ 根据条件 $P_{n}^{'''} (x_{0}) = f^{'''} (x_{0})$ ，我们得到 $3! a_{3} = f^{'''} (x_{0})$ ，即： $a_{3} = \frac{f ^{'''} ( x _{0} )}{3 !}$

5. 寻找规律：求 $a_{k}$

我们发现了一个清晰的规律：

$a_{0} = \frac{f ^{(0)} ( x _{0} )}{0 !}$ (约定 $0! = 1$ 且 $f^{(0)}$ 为 $f$ 本身)
$a_{1} = \frac{f ^{(1)} ( x _{0} )}{1 !}$
$a_{2} = \frac{f ^{(2)} ( x _{0} )}{2 !}$
$a_{3} = \frac{f ^{(3)} ( x _{0} )}{3 !}$

我们可以用数学归纳法证明，对于任意的 $k$ 阶导数（ $k \leq n$ ）： $P_{n}^{(k)} (x) = k (k - 1) \dots (1) a_{k} + (一些包含 (x - x_{0}) 的项)$ $P_{n}^{(k)} (x) = k! a_{k} + (...)$ 将 $x = x_{0}$ 代入： $P_{n}^{(k)} (x_{0}) = k! a_{k}$ 根据我们的第 $k$ 步条件 $P_{n}^{(k)} (x_{0}) = f^{(k)} (x_{0})$ ，得到： $k! a_{k} = f^{(k)} (x_{0})$ 解得： $a_{k} = \frac{f ^{(k)} ( x _{0} )}{k !}$

总结：泰勒公式的诞生

我们已经求出了所有的系数 $a_{0}, a_{1}, \dots, a_{n}$ 。把它们代回到 $P_{n} (x)$ 的表达式中，就得到了这个“最佳替身”多项式，我们称之为 $n$ 阶泰勒多项式 (Taylor Polynomial)： $T_{n} (x) = f (x_{0}) + f^{'} (x_{0}) (x - x_{0}) + \frac{f ^{''} ( x _{0} )}{2 !} (x - x_{0})^{2} + \dots + \frac{f ^{(n)} ( x _{0} )}{n !} (x - x_{0})^{n}$ $T_{n} (x) = k = 0 \sum n \frac{f ^{(k)} ( x _{0} )}{k !} (x - x_{0})^{k}$

这个 $T_{n} (x)$ 只是 $f (x)$ 的一个近似值。它们之间是有误差的。我们把这个误差（或称为“余项”）记为 $R_{n} (x)$ ： $R_{n} (x) = f (x) - T_{n} (x)$

那么， $f (x)$ 就可以被精确地写成： $f (x) = T_{n} (x) + R_{n} (x)$ $f (x) = k = 0 \sum n \frac{f ^{(k)} ( x _{0} )}{k !} (x - x_{0})^{k} + R_{n} (x)$

这就是泰勒公式！

后续的数学家（如拉格朗日、佩亚诺等）的工作，就是去研究这个余项 $R_{n} (x)$ 到底长什么样子、它有多大，从而得到了拉格朗日余项和佩亚诺余项等不同形式。但泰勒公式本身（即那个多项式部分）的推导，就是基于上述“让导数逐阶相等”的构造性思想。

二、佩亚诺型余项泰勒公式 (定义)

我们用 $T_{n} (x)$ 逼近 $f (x)$ 产生的误差项称为余项 $R_{n} (x) = f (x) - T_{n} (x)$ 。

佩亚诺型余项泰勒公式（如图片 image_8b4f3a.png 中 定理 6.9 所示）精确地描述了当 $x$ 趋近于 $x_{0}$ 时，这个误差项 $R_{n} (x)$ 的性质。

定理 (佩亚诺余项)： 如果函数 $f (x)$ 在 $x_{0}$ 处存在直到 $n$ 阶的导数，那么有： $f (x) = T_{n} (x) + R_{n} (x)$ 即： $f (x) = k = 0 \sum n \frac{f ^{(k)} ( x _{0} )}{k !} (x - x_{0})^{k} + o ((x - x_{0})^{n})$ 其中余项 $R_{n} (x) = o ((x - x_{0})^{n})$ 。

核心解析：

$o ((x - x_{0})^{n})$ 意味着 $lim_{x \to x_{0}} \frac{R _{n} ( x )}{( x - x _{0} ) ^{n}} = 0$ 。
这说明佩亚诺余项 $R_{n} (x)$ 是一个当 $x \to x_{0}$ 时，比 $(x - x_{0})^{n}$ 更高阶的无穷小。
通俗地说，这个公式告诉我们，用 $n$ 阶泰勒多项式 $T_{n} (x)$ 去逼近 $f (x)$ ，其误差 $R_{n} (x)$ 会比我们保留的最后一项 $(x - x_{0})^{n}$ 消失得“快得多”。这是一种局部的、定性的误差描述，非常适合用来求极限。

特例：麦克劳林 (Maclaurin) 公式

当 $x_{0} = 0$ 时，泰勒公式就变成了麦克劳林公式（如图片 image_8b4f5f.png 中公式 (6) 所示）。这是实际应用中最常见的形式： $f (x) = f (0) + f^{'} (0) x + \frac{f ^{''} ( 0 )}{2 !} x^{2} + \dots + \frac{f ^{(n)} ( 0 )}{n !} x^{n} + o (x^{n})$

图片 image_8b4f5f.png 中列出了一些必须熟记的麦克劳林公式：

$e^{x} = 1 + x + \frac{x ^{2}}{2 !} + \dots + \frac{x ^{n}}{n !} + o (x^{n})$
$sin x = x - \frac{x ^{3}}{3 !} + \frac{x ^{5}}{5 !} - \dots + (- 1)^{m - 1} \frac{x ^{2 m - 1}}{( 2 m - 1 )!} + o (x^{2 m})$
$cos x = 1 - \frac{x ^{2}}{2 !} + \frac{x ^{4}}{4 !} - \dots + (- 1)^{m} \frac{x ^{2 m}}{( 2 m )!} + o (x^{2 m + 1})$
$ln (1 + x) = x - \frac{x ^{2}}{2} + \frac{x ^{3}}{3} - \dots + (- 1)^{n - 1} \frac{x ^{n}}{n} + o (x^{n})$
$(1 + x)^{α} = 1 + αx + \frac{α ( α - 1 )}{2 !} x^{2} + \dots + \frac{α ( α - 1 ) \dots ( α - n + 1 )}{n !} x^{n} + o (x^{n})$
$\frac{1}{1 - x} = 1 + x + x^{2} + \dots + x^{n} + o (x^{n})$

三、图中例题解析 (image_8b5224.png)

例 2：利用代换法求麦克劳林公式及导数

题目： 写出 $f (x) = e^{- \frac{x ^{2}}{2}}$ 的麦克劳林公式，并求 $f^{(98)} (0)$ 与 $f^{(99)} (0)$ 。

解析：

套用公式： 我们已知 $e^{t}$ 的麦克劳林公式： $e^{t} = 1 + t + \frac{t ^{2}}{2 !} + \frac{t ^{3}}{3 !} + \dots + \frac{t ^{n}}{n !} + o (t^{n})$
变量代换： 令 $t = - \frac{x ^{2}}{2}$ 。 $e^{- \frac{x ^{2}}{2}} = 1 + (- \frac{x ^{2}}{2}) + \frac{( - \frac{x ^{2}}{2} ) ^{2}}{2 !} + \dots + \frac{( - \frac{x ^{2}}{2} ) ^{n}}{n !} + o ((- \frac{x ^{2}}{2})^{n})$
整理： $e^{- \frac{x ^{2}}{2}} = 1 - \frac{x ^{2}}{2} + \frac{x ^{4}}{2 ^{2} \cdot 2 !} - \frac{x ^{6}}{2 ^{3} \cdot 3 !} + \dots + (- 1)^{n} \frac{x ^{2 n}}{2 ^{n} \cdot n !} + o (x^{2 n})$ 这就是所求的麦克劳林公式。
求导数值： 根据麦克劳林公式的定义， $x^{k}$ 项的系数 $a_{k}$ 必须等于 $\frac{f ^{(k)} ( 0 )}{k !}$ 。
- 求 $f^{(99)} (0)$ ： 在我们推导出的 $e^{- \frac{x ^{2}}{2}}$ 展开式中，所有 $x$ 的幂次都是偶数 ( $x^{2 n}$ )。 $x^{99}$ (奇次项) 的系数 $a_{99}$ 显然为 0。因此， $\frac{f ^{(99)} ( 0 )}{99 !} = 0$ ，解得 $f^{(99)} (0) = 0$ 。
- 求 $f^{(98)} (0)$ ： 我们需要 $x^{98}$ 项的系数。令 $2 n = 98$ ，解得 $n = 49$ 。 $x^{98}$ 项的系数 $a_{98} = \frac{f ^{(98)} ( 0 )}{98 !}$ 。从我们推导的公式中，当 $n = 49$ 时，该项系数为 $\frac{( - 1 ) ^{49}}{2 ^{49} \cdot 49 !} = - \frac{1}{2 ^{49} \cdot 49 !}$ 。令两者相等： $\frac{f ^{(98)} ( 0 )}{98 !} = - \frac{1}{2 ^{49} \cdot 49 !}$ 。解得 $f^{(98)} (0) = - \frac{98 !}{2 ^{49} \cdot 49 !}$ 。

例 3：利用代换法求泰勒公式 ( $x_{0} \neq = 0$ )

题目： 求 $ln x$ 在 $x = 2$ 处的泰勒公式。

解析：

目标： 我们需要一个关于 $(x - 2)$ 幂次的展开式。
转化： 我们已知的公式是 $ln (1 + t)$ 在 $t = 0$ 处的展开。我们必须把 $ln x$ 凑成 $ln (1 + t)$ 的形式。
代数变形： $ln x = ln (2 + (x - 2))$ 提出 $x_{0} = 2$ ： $ln x = ln [2 \cdot (1 + \frac{x - 2}{2})]$ 利用对数律 $ln (ab) = ln a + ln b$ ： $ln x = ln 2 + ln (1 + \frac{x - 2}{2})$
变量代换： 现在，我们可以对第二项使用 $ln (1 + t)$ 的麦克劳林公式，令 $t = \frac{x - 2}{2}$ 。已知 $ln (1 + t) = t - \frac{t ^{2}}{2} + \dots + (- 1)^{n - 1} \frac{t ^{n}}{n} + o (t^{n})$ 。
代入： $ln x = ln 2 + [(\frac{x - 2}{2}) - \frac{1}{2} (\frac{x - 2}{2})^{2} + \dots + \frac{( - 1 ) ^{n - 1}}{n} (\frac{x - 2}{2})^{n}] + o ((\frac{x - 2}{2})^{n})$
整理 (可选)： $ln x = ln 2 + k = 1 \sum n \frac{( - 1 ) ^{k - 1}}{k \cdot 2 ^{k}} (x - 2)^{k} + o ((x - 2)^{n})$ 注意： $o ((\frac{x - 2}{2})^{n})$ 与 $o ((x - 2)^{n})$ 是等价的。

例 4：利用泰勒公式求极限

题目： 求极限 $lim_{x \to 0} \frac{c o s x - e ^{- \frac{x ^{2}}{2}}}{x ^{4}}$ 。

解析： 这是一个 $0/0$ 型极限。如果使用洛必达法则，需要求导 4 次，极其繁琐。泰勒公式是最佳方法。

确定阶数： 分母是 $x^{4}$ ，我们必须将分子展开到 $x^{4}$ 项，并保留 $o (x^{4})$ 或更高阶的余项。
展开 $cos x$ ： 使用 $cos x$ 的麦克劳林公式，展开到 $x^{4}$ 项 (或更高)： $cos x = 1 - \frac{x ^{2}}{2 !} + \frac{x ^{4}}{4 !} + o (x^{5}) = 1 - \frac{x ^{2}}{2} + \frac{x ^{4}}{24} + o (x^{5})$
展开 $e^{- \frac{x ^{2}}{2}}$ ： 使用例 2 的结果，展开到 $x^{4}$ 项 (即 $n = 2$ )： $e^{- \frac{x ^{2}}{2}} = 1 - \frac{x ^{2}}{2} + \frac{x ^{4}}{2 ^{2} \cdot 2 !} + o (x^{4}) = 1 - \frac{x ^{2}}{2} + \frac{x ^{4}}{8} + o (x^{4})$ (注：更精确地， $e^{t} = 1 + t + t^{2} /2 + o (t^{2})$ ，代入 $t = - x^{2} /2$ 得到 $o ((- x^{2} /2)^{2}) = o (x^{4})$ 。如图中所示，使用 $o (x^{5})$ 也是正确的，因为下一项是 $x^{6}$ 。)
代入分子： $cos x - e^{- \frac{x ^{2}}{2}} = (1 - \frac{x ^{2}}{2} + \frac{x ^{4}}{24} + o (x^{5})) - (1 - \frac{x ^{2}}{2} + \frac{x ^{4}}{8} + o (x^{5}))$ （注意： $o (x^{5}) - o (x^{5}) = o (x^{5})$ ，低阶减高阶等于低阶，例如 $o (x^{4}) - o (x^{5}) = o (x^{4})$ ） $= (1 - 1) + (- \frac{x ^{2}}{2} - (- \frac{x ^{2}}{2})) + (\frac{x ^{4}}{24} - \frac{x ^{4}}{8}) + o (x^{5})$ $= 0 + 0 + (\frac{1}{24} - \frac{3}{24}) x^{4} + o (x^{5})$ $= - \frac{2}{24} x^{4} + o (x^{5}) = - \frac{1}{12} x^{4} + o (x^{5})$
计算极限： $x \to 0 lim \frac{cos x - e ^{- \frac{x ^{2}}{2}}}{x ^{4}} = x \to 0 lim \frac{- \frac{1}{12} x ^{4} + o ( x ^{5} )}{x ^{4}}$ 将 $x^{4}$ 除到分子中： $= x \to 0 lim (- \frac{1}{12} + \frac{o ( x ^{5} )}{x ^{4}})$ $= x \to 0 lim (- \frac{1}{12} + x \cdot \frac{o ( x ^{5} )}{x ^{5}})$ 因为 $lim_{x \to 0} \frac{o ( x ^{5} )}{x ^{5}} = 0$ ，所以 $lim_{x \to 0} (x \cdot \frac{o ( x ^{5} )}{x ^{5}}) = 0 \cdot 0 = 0$ 。 $= - \frac{1}{12} + 0 = - \frac{1}{12}$

四、生成实例及解析

这里为您生成一个类似的、常用于考察佩亚诺余项的极限例题。

实例： 求极限 $lim_{x \to 0} \frac{s i n x - x c o s x}{x ^{3}}$ 。

解析： 这是一个 $0/0$ 型极限。分母为 $x^{3}$ ，因此我们需要将分子中的 $sin x$ 和 $cos x$ 展开，使得分子的最终结果包含 $x^{3}$ 项和余项 $o (x^{3})$ 。

展开 $sin x$ ： 分母是 $x^{3}$ ，我们至少要展开到 $x^{3}$ 项。 $sin x = x - \frac{x ^{3}}{3 !} + o (x^{4}) = x - \frac{x ^{3}}{6} + o (x^{4})$ (保留到 $o (x^{4})$ 或 $o (x^{5})$ 是因为 $sin x$ 的 $x^{4}$ 项系数为 0，更精确)
展开 $x cos x$ ： 我们先展开 $cos x$ 。因为 $cos x$ 前面要乘以一个 $x$ ，所以 $cos x$ 只需要展开到 $x^{2}$ 项，就能得到 $x^{3}$ 项。 $cos x = 1 - \frac{x ^{2}}{2 !} + o (x^{3}) = 1 - \frac{x ^{2}}{2} + o (x^{3})$ 现在，乘以 $x$ ： $x cos x = x (1 - \frac{x ^{2}}{2} + o (x^{3})) = x - \frac{x ^{3}}{2} + x \cdot o (x^{3}) = x - \frac{x ^{3}}{2} + o (x^{4})$
代入分子： $sin x - x cos x = (x - \frac{x ^{3}}{6} + o (x^{4})) - (x - \frac{x ^{3}}{2} + o (x^{4}))$ $= (x - x) + (- \frac{x ^{3}}{6} - (- \frac{x ^{3}}{2})) + (o (x^{4}) - o (x^{4}))$ $= 0 + (- \frac{1}{6} + \frac{3}{6}) x^{3} + o (x^{4})$ $= \frac{2}{6} x^{3} + o (x^{4}) = \frac{1}{3} x^{3} + o (x^{4})$
计算极限： $x \to 0 lim \frac{sin x - x cos x}{x ^{3}} = x \to 0 lim \frac{\frac{1}{3} x ^{3} + o ( x ^{4} )}{x ^{3}}$ $= x \to 0 lim (\frac{1}{3} + \frac{o ( x ^{4} )}{x ^{3}})$ $= x \to 0 lim (\frac{1}{3} + x \cdot \frac{o ( x ^{4} )}{x ^{4}})$ $= \frac{1}{3} + 0 \cdot 0 = \frac{1}{3}$

好的，为了辅助您学习泰勒公式，我将生成一张图片，通过可视化方式展示函数及其泰勒多项式逼近的效果。

这张图将展示一个函数 (例如 $e^{x}$ ) 及其在某一点 ( $x_{0} = 0$ ) 处的低阶泰勒多项式（1阶、2阶、3阶）的图像，让您直观地看到随着阶数增加，泰勒多项式如何更好地逼近原函数。

alt text

尽管如此，我仍然可以为您提供一个文本描述，详细说明这张图应该包含的所有中文信息和解释，您可以根据这个描述来理解图像所要表达的概念。

优化图片内容的中文文本描述 (理想图像应包含的内容):

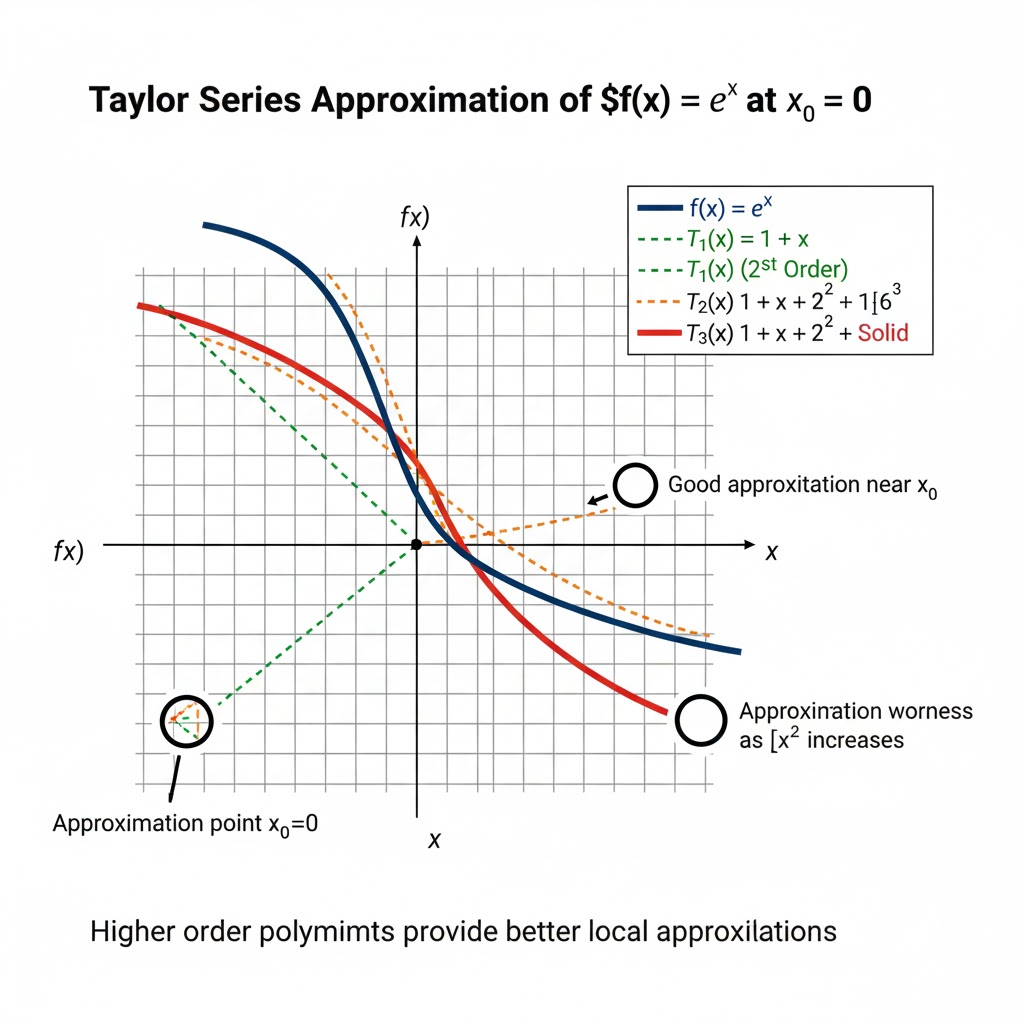
图片标题： 函数 $f (x) = e^{x}$ 在 $x_{0} = 0$ 处的泰勒级数逼近

图例：

深蓝色实线： $f (x) = e^{x}$ (原函数)
绿色虚线： $T_{1} (x) = 1 + x$ (一阶泰勒多项式/切线)
橙色虚线： $T_{2} (x) = 1 + x + \frac{1}{2 !} x^{2}$ (二阶泰勒多项式)
红色粗实线： $T_{3} (x) = 1 + x + \frac{1}{2 !} x^{2} + \frac{1}{3 !} x^{3}$ (三阶泰勒多项式) (注：图例中可以根据需要展示更多阶，例如四阶、五阶，但为了清晰，通常展示到三阶或四阶)

图像标注：

在 $x$ 轴原点处 (或 $x_{0} = 0$ 处)： “逼近点 $x_{0} = 0$ ”
箭头指向 $x_{0} = 0$ 附近区域： “在 $x_{0}$ 附近，逼近效果极佳”
箭头指向远离 $x_{0} = 0$ 的区域（左右两边）： “远离 $x_{0}$ ，逼近效果逐渐变差”

底部总结语： “阶数越高，泰勒多项式在逼近点附近的逼近效果越好”

核心概念解释： 这张图的目的是直观展示泰勒公式的核心思想：

局部逼近： 泰勒多项式是函数在某一点附近的局部良好逼近。
阶数与精度： 随着泰勒多项式阶数的增加，它与原函数在逼近点附近的重合度越高，逼近精度越好。
远离逼近点： 即使是高阶泰勒多项式，在远离逼近点 $x_{0}$ 的区域，其与原函数的偏差也会增大，逼近效果会显著变差。

Keyboard shortcuts

万物之理：从计数到宇宙的数学地图